通过 真值表 直接构建 异或门
现在来探讨一下一种机械的方法论, 通过它能够设计出任何的组合逻辑电路.
不过在深入探讨这个问题之前, 需要对现有的基础门电路的特性有一个比较好的理解与掌握.
非门的特性
先来看非门的特性, 非门的存在, 使得我们一旦能得出某组结果, 也一定能得出相反的结果.
比如, 异或门的四种输出结果是 0 1 1 0. 反一下就有 1 0 0 1.
这里假设输入总是按 00, 01, 10, 11 的顺序.
所以, 如果 0 1 1 0 能够实现, 1 0 0 1 就一定也能实现. 不过, 在模式之外的呢? 比如 1 0 1 0, 它不是任何你知道的现有的门电路的反向. 这种情况你该怎么办?
注: 就 1 0 1 0 而言, 它其实可以是输入 B 的反向, 也即只需要对一个输出 B 取反, 输入 A 则完全丢弃即可. 你可以通过真值表验证这一点:
A B Y 0 0 1 0 1 0 1 0 1 1 1 0
这里需要首先谈下另外两种基本的门电路, 也就是 与门 和 或门 的一些特性.
与门的特性
与 也即是串联. 串联有一个特性, 多个开关, 如果想最终输出高电平, 则所有开关都需要闭合.

反过来, 如果看到一个串联电路输出了高电平, 可以反推出所有的开关都是闭合的.
也即是如果有表达式 A & B = 1, 那么 一定且只能 是 A = 1; B = 1.
所有 A 跟 B 的其它组合, 比如 A = 0; B = 0, 或是 A = 0; B = 1, 或是 A = 1; B = 0, 它们都不可能令 A & B = 1, 并且一定会导致 A & B = 0.
这是由串联电路的特性 有一个开关断开, 整个电路就是低电平 所决定的.
同理, 如果有表达式 !A & B = 1, 那么一定且只能是 A = 0; B = 1.
注: 这里
!A指对 A 取反, 见前面的相关介绍.另注: 取反操作具有最高的优先级, 就像一般的算术表达式里, 乘法的优先级高于加法那样. 上述表达式表示先对 A 取反, 再跟 B 取与.
所有其它的组合, 比如 A = 0; B = 0, 或是 A = 1; B = 0, 或是 A = 1; B = 1, 它们都不可能令 !A & B = 1, 而是一定会导致 !A & B = 0.
这个结论可以进一步扩展到三个或以上输入的情况. 也即是如果有表达式 A & B & C = 1, 那么 一定且只能 是 A = 1; B = 1; C = 1; 其它组合的结果均为 0.
以上就是 与门 的特性.
或门的特性
不同于 与门 的严苛特性, 或门的逻辑里, 有一个 1(高电平), 结果就是 1(高电平).
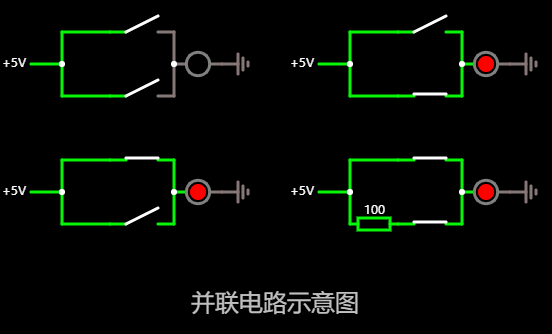
或 也即是并联.
如果有表达式 A | B = 1, 那么可以是 A = 1; B = 任何值, 或者是 B = 1; A = 任何值.
注: 这里竖线
|指对两个输入取或, 见前面的相关介绍.
这个结论对于复合的表达式也是成立的. 比如如果有表达式 (A & B) | (!A & B) = 1, 那么可以是其中一个子表达式 A & B = 1 或者是另一个子表达式 !A & B = 1.
注: 为避免歧义, 复合的表达式里使用了括号, 括住的两个子表达式先运算, 最后两个子表达式的结果再进行 或 运算. 也即最外层是或运算, 里层两个则是与运算.
异或门的表达式
有了前述基础, 通过求解异或门表达式这个具体实例来阐述这样的机械方法论. 先说步骤与结论, 再分析为什么是可行的.
第一步是列出异或门的真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
第二步是留下那些 Y 的值是 1 的行, 对于异或门的例子, 也就是中间两行:
| A | B | Y |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 0 | 1 |
第三步是在留下的行里, 写出每一行中, 使 A B 输出的值为 1 的 与组合 表达式.
比如, 第一行, A = 0, B = 1, 然后要 Y = 1, 则 与组合 表达式只能是
!A & B;同理, 第二行, A = 1, B = 0, 然后要 Y = 1, 则 与组合 表达式只能是
A & !B;
有多少行就写多少个.
另: 这里示例是两个输入 A 和 B 的情况, 如果有更多输入, 比如 A B C 三个, 那么就写三个输入的 与组合 表达式.
第四步, 将第三步得到的全部 子表达式 用 或组合 组合起来, 就是最终的结果.
对于异或门的实例, 即是 Y = (!A & B) | (A & !B).
整个顺序是:
- 各个输入, 看情况或是保持原样, 或是用 非门 取反;
- 再用 与门 对全部输入的组合 取与,
- 最后把多个取与的结果用 或门 取或.
根据这个表达式, 最终搭建的电路如下:
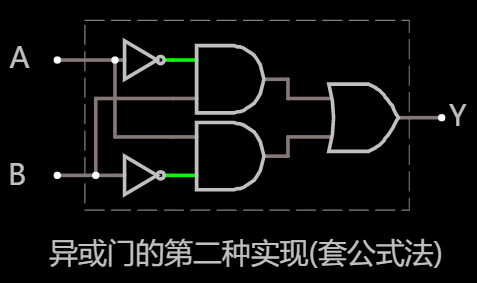
为什么可行?
现在分析下为什么用上述方式得出的表达式可以满足需求.
其实最简单的方式还是列出真值表:
| A | B | Y | !A | (!A & B) = X | !B | (A & !B) = Z | X | Z |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
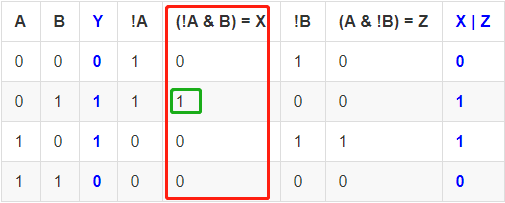
再逐个分析. 根据前面对与门特性的分析, 第一个子表达式 !A & B 是针对第一个结果为 1 的输入制定的, 在表里也就是第二行, 因此, 其它几行里, 它的结果都是 0.
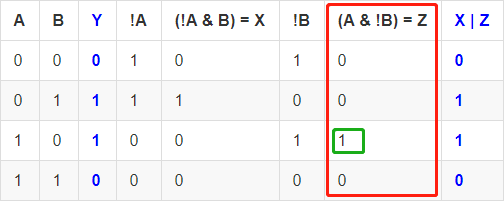
同理, 第二个子表达式 A & !B 是针对第二个结果为 1 的输入制定的, 在表里也就是第三行, 因此, 其它几行里, 它的结果都是 0.
现在分析第一行的情况, 显然, 因为 Y = 0, 而前面只针对 Y = 1 的情况去筛选并书写输入的 求与 子表达式, 因为两个子表达式都不是针对它的输入情况去制定的, 因此两个子表达式的结果均为 0, 最后 0 | 0 的结果还是 0, 满足要求.
第二行的情况, 显然, 因为 Y = 1, 所以有一个子表达式是针对它的, 结果能得到 1, 也即是 !A & B = 1; 另一个子表达式 A & !B 在这里的结果依旧是 0; 但最后因为有一个 1, 1 | 0 的结果还是 1, 这是 或门 特性决定的, 结果满足要求.
第三行情况, 与第二行同理, 最后是 0 | 1 结果也还是 1, 满足要求.
第四行, 与第一行情况类似, 因为两个子表达式也都不是针对它的输入情况去制定的, 子表达式结果必然都是 0, 最后 0 | 0 的结果还是 0, 满足要求.
经测试, 所搭建的电路是满足真值表要求的:
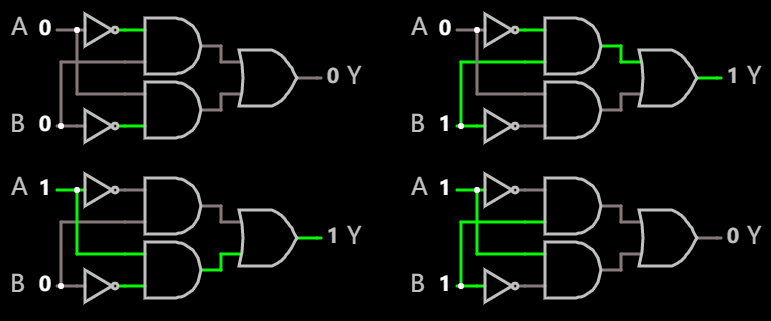
分析至此, 不难看出, 通过这样的先用非门对输入取反(或保持原样), 再用与门把输入的组合 取与, 最后把多个取与的结果用或门 取或 的方式, 在表达所需逻辑上是没有问题的.
可行性问题也因此迎刃而解.
此外, 这里举的示例虽然只是两个输出, 同时总的规则只有四条的情况, 但不难看出, 这个结论是完全可以进一步推广至更多的输入(三个, 四个或是更多均可), 以及更多的规则(五条, 六条甚至更多)的.
在前面, 曾经做过输出的 LED 数码管译码, 我们是用各种或是启发式, 或是采用分而治之等方式简化后才终于得以解决的. 现在, 掌握了上述机械的方法论, 解决起来就简单了.
为更好掌握此种方式, 在下一篇中将应用它重新实现译码电路.